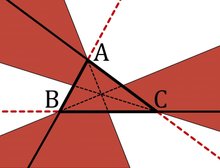
This package consists of MATLAB functions for calculating displacements, strains and stresses associated with triangular dislocations (TDs) in a homogeneous elastic full-space or half-space. The functions implement the Nikkhoo and Walter (2015) analytical solutions that are free of artefact singularities and numerical instabilities. These solutions are also independent of the model scale and can thus be applied to a wide range of problems in geophysics, engineering and physics, without requiring any alterations in the input data or the geometry of meshes of the TDs.

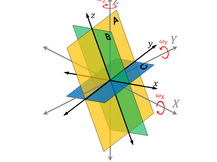
This package contains MATLAB functions for calculating displacements, strains and stresses associated with rectangular dislocations (RDs), compound dislocation models (CDMs) and generalized point sources of pressure in a homogeneous elastic full-space or half-space. The functions implement the Nikkhoo et al. (2017) analytical solutions and the Eshelby (1957) shape tensor.

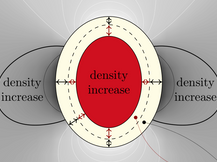
This package contains MATLAB functions for calculating gravity changes associated with triaxial volumetric sources of expansion, namely, the point Compound Dislocation Model (point CDM) and point Ellipsoidal Cavity Model (point ECM) in a uniform elastic half-space. The functions implement the Nikkhoo and Rivalta (2022a) analytical solutions, which build on the Okubo (1991) and Eshelby (1957) analytical solutions.

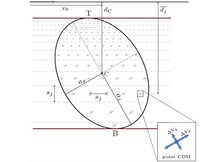
This package contains MATLAB functions for calculating surface deformations (displacements, strains, tilts) and gravity changes caused by uniformly-pressurized finite triaxial ellipsoidal cavities, namely, the finite Ellipsoidal Cavity Model (finite ECM) in a uniform elastic half-space. The functions implement the Nikkhoo and Rivalta (2022b) quasi-analytical solutions, which build on the Nikkhoo and Rivalta (2022a) , Okubo (1991) and Eshelby (1957) analytical solutions.